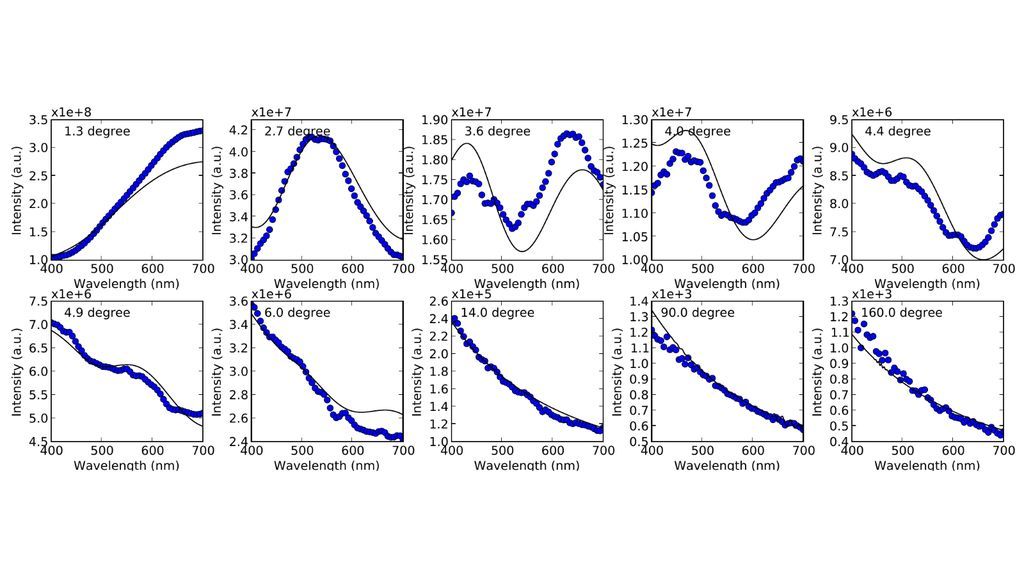
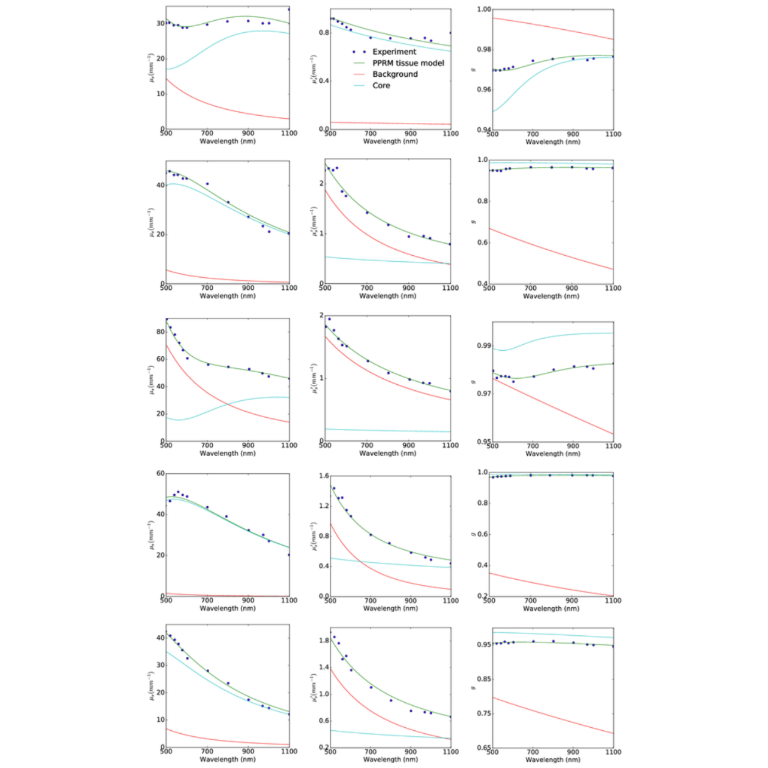
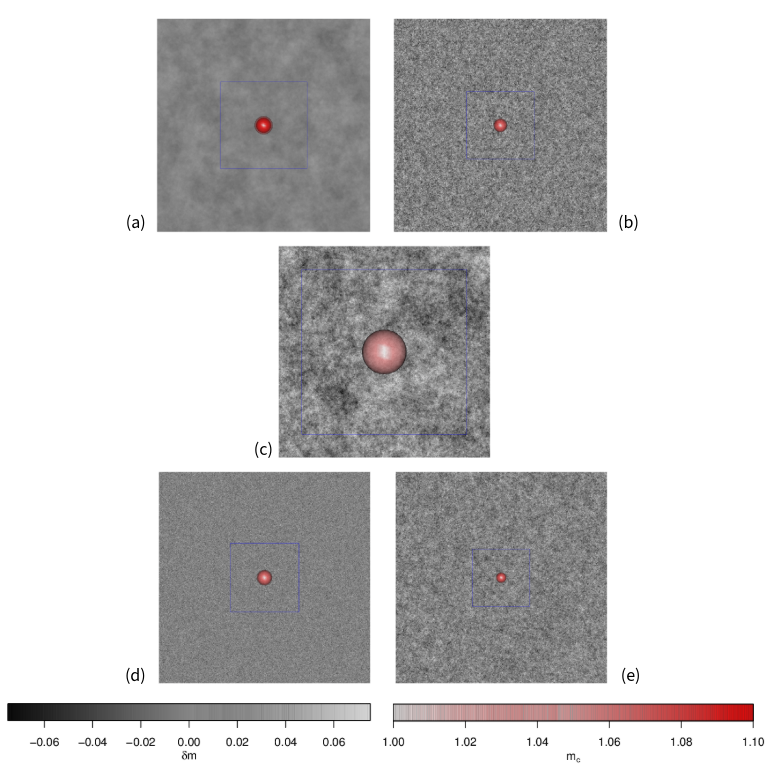
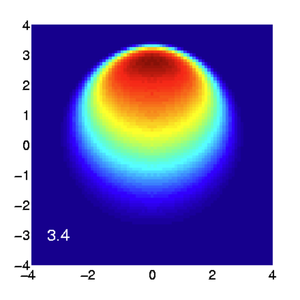
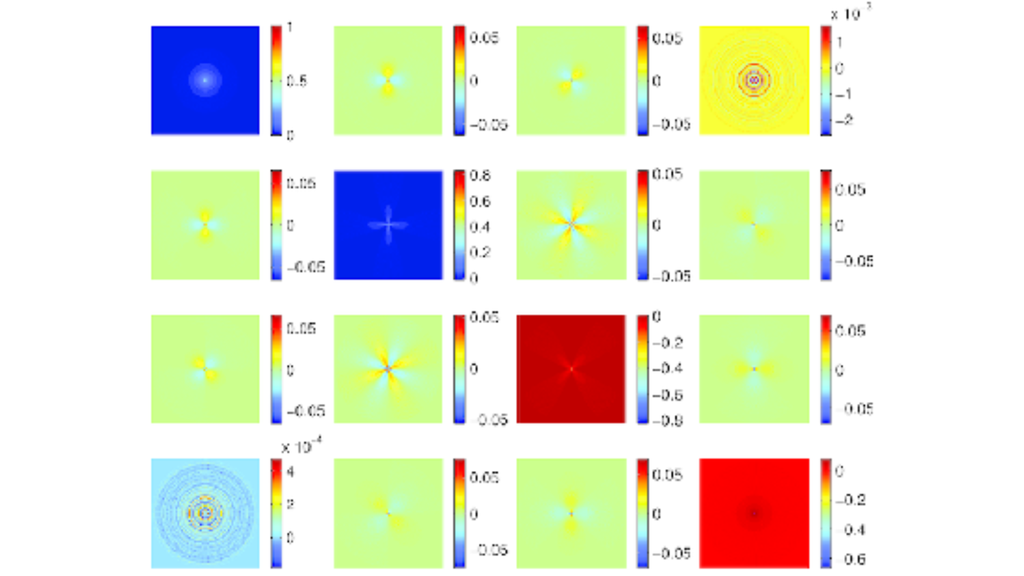
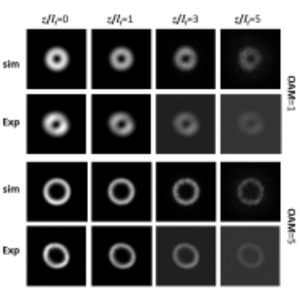
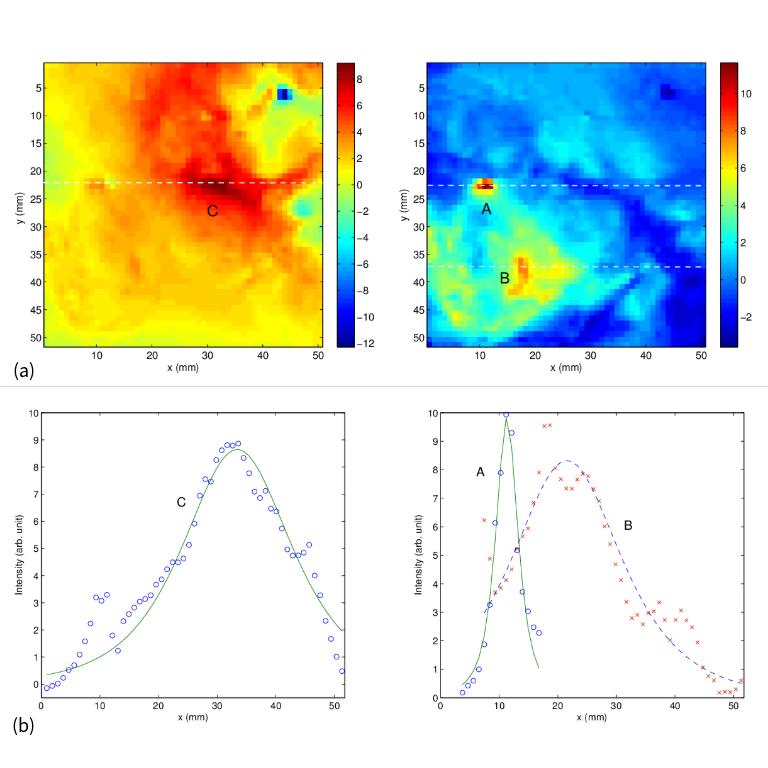
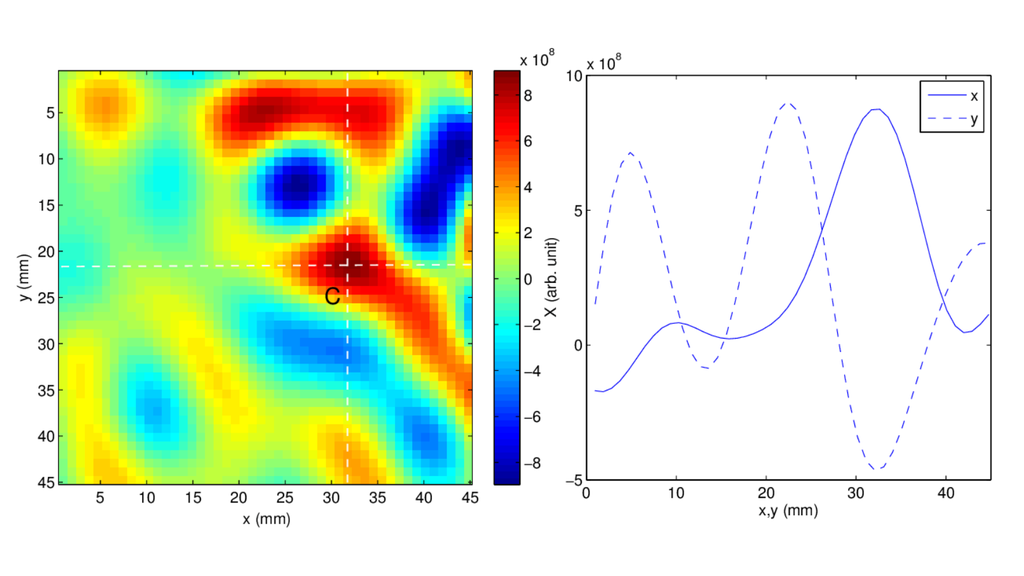
Overview
The quest for the physics of light-turbid soft matter (e.g., biological tissue and cells) interaction and the endeavor in engineering for noninvasively characterization and diagnosis of tissue and cells with light at the interface of physics, engineering and biomedical sciences are the current central themes of Biomedical Photonics Laboratory @ Hunter. With the recent advances in light sources, manipulation devices, and detectors as well as the ever-increasing computational power, biophotonics has attracted significant interest and is well positioned to tackle unmet needs and challenges in health-related imaging, monitoring and diagnosis. Biomedical Photonics Laboratory is devoted to address fundamental problems and make innovations in this exciting field with integrated analytical, computational, and experimental approaches.